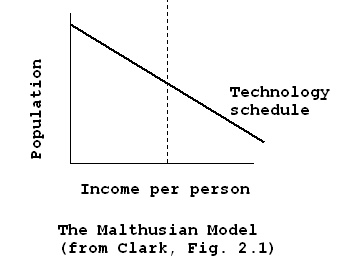
The Malthusian model is not as crazy as Greg Clark’s interpretation of it in A Farewell to Alms (here’s Clark’s reply; here’s my rebuttal, with a second reply from Clark in the comments). But even correctly interpreted, the Malthusian model is deeply flawed.
A key assumption of the Malthusian model is that when population goes up, average living standards go down.

Intuitively, this make sense: When more people share a pie, each slice gets thinner. And in the short-run, this Malthusian assumption is clearly correct. When a couple has its first child, the family’s per-capita income plummets by one-third. Clark documents, similarly, that when repeated plagues cut England’s population in half, living standards for the survivors roughly doubled.
But here’s the problem: As Michael Kremer and especially Julian Simon explain, there are powerful long-run effects of higher population that go in the opposite direction. Most notably:
1. More people increase both the supply and demand for new ideas.
2. More people make it possible to exploit economies of scale – including scale economies of transportation and communication.
3. Since human diversity rises with human population, more people allow for efficiency gains from specialization and trade.
These effects could easily suffice to overpower the Malthusian diminishing marginal returns effect, so the right diagram looks like:
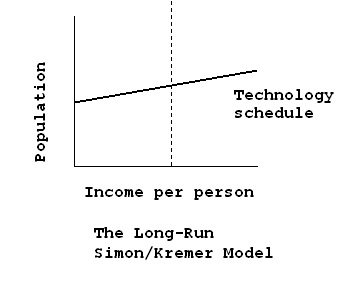
If this seems implausible, imagine a world populated by a million immortal, sterile human beings at the hunter-gatherer level. There’s plenty of land per person, but that’s hardly enough to give you the Internet, the airplane, German opera, or any of the countless wonders that we take for granted. How long would it take these million immortals to invent our standard of living? Would the sun burn out first?
A Farewell to Alms briefly acknowledges population benefit #1: “There is clearly a core of sense to the idea that increased population size, the product of past technological change in the preindustrial era, increased the rate of technological advance.” (p.228) In comments on this blog, Clark makes the point more strongly: “And indeed the book accepts that one of the things bringing about the Industrial Revolution was the much greater population of the world in 1800 than in 100,000 BC.” But this admission plays almost no role in Clark’s larger story – and it absolutely should.
Once you accept the long-run benefits of higher population, praising the Black Death for raising the average standard of living is severely myopic. Halving the population may double the standard of living of the survivors in the short-run. But in the long-run, a smaller population delays the arrival of modernity. On Clark’s account, it took England about two centuries to return to its pre-plague population. On his own terms, then, it is entirely possible that – but for the plague – the Industrial Revolution would have begun two centuries earlier.
In fact, once you take the long-run benefits of population on living standards seriously, the “Malthusian trap” takes on an new cast. Perhaps the real trap is that you have to be pretty rich to keep a big population alive long enough to reap the long-run benefits of a big population. For the pre-modern era, this story fits the facts as well as Clark’s, but it has the added virtue that it fits the facts of the modern era as well.
Update: Clark responds in the comments.

READER COMMENTS
Steve Sailer
Oct 7 2007 at 4:32pm
Okay, but before 1800, China, India, and Japan all had vastly larger populations than England, but no Industrial Revolution. Indeed, China was moving backward technologically during 1500-1800 despite population numbers reaching unprecedented heights. (Japan was making modest progress forwards.) Perhaps the vast pressure of population led to stultification in China — experimentation was frowned upon because if something went wrong, tens of millions of people died. The lower population density of the English (due to mostly to later marriage) meant there was more margin for error, so more experimentation.
Felix
Oct 7 2007 at 6:32pm
Arguments that figure the Black Plague to be good for living standards seem odd.
Consider this: If everyone in the world but you dies this instant, your living standard goes way, way up. Hey, any yacht you want is there for the taking! So this imaginary, massive die-off seems to confirm the Malthusian world view. It’s so easy to not count the living standards of the people who died.
And, let’s consider the assertion that England took two centuries to catch up to its living standards, pre-plague. First, let’s go out on a limb here and speculate that English parents don’t like their babies to die young. Let’s also speculate that people are attracted to behaviors that produce babies (pre birth control pill). Now, given those speculations, why did the population of England not pop back up in a generation to its pre-plague level? After all, from a Malthusian point of view, the country should have been able to “support” such a population. Here are some reasons:
1) Babies rarely died. There simply weren’t enough mothers.
2) The country wasn’t the same country. Different weather, for instance.
3) Living standards weren’t so hot after all, even without including the living standard of those dead babies.
4) There may have been a slight delay in over-all procreation numbers since healthy young adults were disproportionately killed by the plague.
Felix
Oct 7 2007 at 6:33pm
What seems true is that larger populations are necessary for better living conditions. But they are not sufficient. It seems that, for Matcalf’s Law to apply, the people must be connected. Or, to put it in less techie terms, more cooperative.
Steve Sailer
Oct 7 2007 at 6:54pm
Clark’s basic point is that the world began to change profoundly around 1800 in one place, and then spread from there. Julian Simon’s theories may or may not be true for the modern world, but the world before the Industrial Revolution was very different, and Malthus described it with a lot of accuracy.
Steve Sailer
Oct 7 2007 at 7:01pm
“Now, given those speculations, why did the population of England not pop back up in a generation to its pre-plague level?”
Because the English practiced a lot of population control through self-discipline. The average marriage age was 24-26, 10%-25% of women never married, and the illegitimacy rate through was in the low single digits. Jane Austen novels give a clear picture of how dependent getting married was on having some money. In other words, the Malthusian trap wasn’t as severe in England as it could be because English women already did what the Rev. Malthus advised them to: practice sexual self-discipline until they could afford a family.
In contrast, Chinese women typically married as teenagers, and almost all married. So, the population would shoot up rapidly, then collapse during periods of bad government. So, as Malthus said, the Malthusian trap was tighter in China than in England.
Steve Sailer
Oct 7 2007 at 7:10pm
I know that Julian Simon is some kind of infallible guru, but there are lots of historical examples of large populations retarding innovation. For example, Egypt had a large population, but basically stopped innovating around 2500 BC, and since only briefly took it up again in the Greek city of Alexandria for a few centuries.
In contrast, the classical Greeks had relatively low population due to out-colonization, homosexuality, and the use of a now-extinct contraceptive herb. And they were pretty good at innovating!
Felix
Oct 7 2007 at 7:57pm
Hmmm. I get the impression that her novels are about people who were anything but average, median, representative or whatever. And were a bit later than the 13 to 16 hundreds.
But that is interesting – that English farm girls didn’t have kids until they were in their mid-twenties, while Chinese farm girls had theirs right after menarche (presuming both sets of girls’ ages of menarche were similar). I say, “farm girls” because any others were too few in number to affect the stats. … Kind of like saying “slaves” instead of “classical Greeks”, right?
Steve Sailer
Oct 7 2007 at 10:15pm
In contrast, the Census of 1801 found that the population of Britain was 8.9 million, or about 1/40th to 1/50th that of China. Yet, which country was creating more new and useful ideas at that point?
Felix
Oct 7 2007 at 11:52pm
Wow! Those sure are big ratios. I’m a little surprised by the Britain population number, as it’s not a particularly big multiple over the US at the time. But, what’s a few million here or there when they are down 40 to 1? 🙂
So, then so far as innovation is concerned, it does appear that Britain had a lot of leverage on their assets, so to speak. If the key is population-connectivity, then the implication is that the people of China, though we may think of them as a bloc, may have been pretty disconnected from each other, if not the rest of the world. Furthermore, I’m guessing that many English of 1800 had some (relatively) tight connections outside England, let alone inside. England at the time did not stand alone, that’s for sure. If Western Europe sank in to the ocean in 1800, England may have been in a bit of a pickle, even with all those connections to the rest of the world.
Or another way of saying it is, it may be cheating to count just England alone in comparison to China. Isn’t that kind of like saying, “Look at the amount of innovation going on at MIT! Why isn’t the same thing going on in Kansas, which has a much higher population than MIT?”
I mean that in the sense of specialization rather than, “But MIT draws people from Kansas, whereas…”. Ah, maybe it’s a bad analogy – factually incorrect, but true, Mr. Rather.
Well, who knows? Maybe a positive mental attitude is necessary, too. 🙂
Steve Sailer
Oct 8 2007 at 12:26am
The Chinese had a centralized empire, with a meritocratically selected bureaucracy. I believe, although I’m not certain, that the mandarins were sent to other parts of the country to prevent local hereditary power bases from growing up. They had good river and canal connectivity to most of the heavily populated parts of China.
They just weren’t inventing stuff anymore, whether technology or even the arts. The same was true for India and the Arab world. Outside of Europe and, to a lesser extent, Japan (and possibly the New World), the world was just marking time after about 1500 AD.
Jason Malloy
Oct 8 2007 at 2:32am
– Charles Murray, Human Accomplishment, p 310.
Datacentric conclusion from Chapter 14, ‘Taking Population into Account’.
Steve Sailer
Oct 8 2007 at 6:52am
Indeed, it’s very odd, the distribution of greatness. For awhile, Beethoven, Mozart, and Haydn all lived in little Vienna at the same time. Now the city is ten times bigger, but there aren’t 30 composers of that quality there now.
Bryan Caplan
Oct 8 2007 at 12:29pm
Here’s is a response from Greg Clark. All that follows is his.
Malthusian Myopia – Clark Response
Bryan accepts that the technology schedule portrayed in the book (figure 2.1) is the one that holds for the short run in the pre-industrial world.
But he argues that the rate of outward shift of that curve in the long run is determined in part by the size of the population in a variety of
ways. It will shift faster the greater the world population. Thus the date at which we arrive at the Industrial Revolution will be in part
determined by the level of the subsistence wage – the lower it was, the greater would be the population, and the sooner the IR would arrive to
liberate mankind. Material deprivation was redemptive before 1800!
This is an interesting possibility, which I do not dismiss out of hand. But here are a some major caveats:
(1) At a very low subsistence wage almost all consumption is of basic foods. Urban areas are small and very few industrial goods are
consumed. The IR was in the first instance (until the late 19th c) largely an industrial phenomenon. Thus the effects of a lower subsistence wage on the size of the industrial population could actually be to shrink the industrial sector, and hence also by Kremer/Simon type processes delay the IR.
Which effect would predominate is an empirical matter.
World population in 1750 was 770 m. (p. 139). Suppose through a lower subsistence wage it was 1,500 m. Would a huge, completely immiserized,
mass of people make an IR any more likely? Or did Western Europe in part have an IR because through the accident of bad hygiene they lived well, had flourishing markets for all kinds of industrial goods, and gained from the scale of those markets and occupations?
(2) Even if Bryan is right, and caveat (1) does not apply, for a given society such as England, which had 6 m of the 770 m people in the
world in 1750, whatever the global growth effects, shrinking your own population would be still highly beneficial. So for all national policy
makers the conclusions of the book would still hold even if I accept Bryan’s reasoning (except perhaps for China).
(3) Even if more people would have speeded up the rate of technological advance and brought an IR more quickly, the trade-off between the date of the IR and living standards in the pre-industrial
world would have been fairly unattractive by most estimates.
Suppose that the population given in table 7.1 (p. 139) had been 50% lower at each date through history. Population in 1750 would then have
been 385 m. English experience suggests that that could have nearly doubled material living standards for mankind from 130,000 BC to AD
1750.
How much later would the IR have been if we just assume that you needed 770 m people to achieve that? Based on population growth rates given in
the table, the IR would then not have taken place till 500 years later.
That would have extended the Malthusian era by 0.38%. Is that an attractive trade-off?
Troy Camplin
Oct 8 2007 at 8:23pm
Malthus only makes sense if there is no growth at all, meaning his ideas do not apply to anything that lives and/or grows. Nor do hs ideas apply to evolving systems. Or to complex systems with emergent properties.
In other words, Malthus’ ideas do not apply to an economy with free market properties. But it would apply to a socialist planned economy.
Felix
Oct 8 2007 at 8:50pm
Slow reader here. It took quite a few readings of that Clark quote to finally get that he’s taking Fig 2.1 seriously.
And, perhaps Bryan does.
I just don’t understand it. That “intuitive” sense works, maybe, if you assume that each human is totally self-sufficient. And that she can be no other way.
But, what’s this “pie”? Where is it?
Look around. Heck, look up in the sky at night. Big pie, no?
Now, take away everything around you that’s created by another human. Don’t do this while driving. Don’t do this indoors. Don’t do this if you live away from a stream. Don’t do this if you are not between the ages of 16 and 30. Don’t do this outside that tropical island paradise.
Ratchet back a few hundred years and do the same. Guess what, buddy. You’re still toast.
Zoom out in time span. Which way does the “income per person” (what a tellingly labeled metric!) curve go from 30,000BC to 1700AD? And the population? I would submit that if you don’t have an upward curve there, you need to go out in the woods for a while, all alone. Without a visit to REI and Safeway first. Heck, go easy on yourself. Take some friends. Take your pregnant wife. Have a ball. Don’t call for help. You can count on Fig. 2.1. Your income will be astounding. It’s intuitive!
Black Plague, drop in English population, good times for a while? Let me look at my cards. Yessss, I see your blip with 1800 to 2000, and raise you the entire world. Oh heck, I’ll use 0 to 2000. Or whenever. Just be sure you count everybody when you count “income”.
Matt
Oct 8 2007 at 9:08pm
Sorry for taking so long to respond.
The issue here is what happened between 1700 and 1750 to give birth to the modern industrial state. Brian says the population increase in the post plague years had a forcing on the economies by virtue of larger population sizes. Brian requires long run measurements, perfectly valid because we are talking about a 50 year period in a 200 year pattern of plague years.
His theory, relativisticly stated, is that economists today, measuring over 50 year period would find a sudden improvement in efficiencies in Europe’s economies around 1700-1750, more or less. The emphasis here is economists measuring over 50 year integration periods.
If Brian’s theory is true, than we have to talk about what the post plague generation was doing to make today’s economists happy today. They either must have been measuring value using a 50 year outlook (my theory), or there must be some inherent stability in larger, or more numerous markets (Brian’s theory).
Demographically we had a post plague educated generation looking out over 30 year careers. They both survived the plague years, but more importantly, their parnets had good confidence by 1700 that they could protect their children from the plague. They were both numerous and had longer outlooks. By 1750 the first modern census was taken and the industrial state had been born.
What is first, economies of scale or longer outlook? I need a measurement that tells us which forcing function is stronger. To be continued?
wcu1291
Oct 8 2007 at 10:48pm
What I find most interesting about the Malthusian short-term and the Simon/Kremer long-term models is that they are both intuitive. Going back to the pie analogy, the more people that share a pie the smaller the slices they receive. One could also apply that to the long-term model; the increasingly smaller portions would drive people to make another, bigger pie to accommodate all of their needs. With regards to England and the Industrial Revolution, its smaller size and separation from the continent gave it a finite amount of land that was suitable for farming. Thus, with a growing population the amount of usable land was decreasing, so it was forced to find another way to support its economy besides agriculture. That is what helped England to have and industrial revolution sooner than other countries with larger populations (like China).
Gordon Clason
Oct 9 2007 at 1:23am
Malthus essentially said that population grows exponentially while development of crop land grows arithmetically, thus population will eventually outstrip available crops. History has proved him wrong because the amount of food one can grow on an acre of land is not a constant, but is dependent on agricultural technology. Applying his apocalyptic conclusions to any scenario that doesn’t include his mistaken mathamatics is a fallacy. Civil engineering in Europe from at least Roman times to today follows a progression in which the Industrial Revolution is only a step, and I would argue a minot one. Roman aquaducts, movable type, many other examples, are at least as innovative as steam power which kicked off the Industrial Revolution. The standard of living in and around the plague is an abberation compared to the slow steady rise in living standards from the time of Martin Luther to Issac Watts. China and Egypt are “river empires” which have different rules and can’t be used as representative. The fall of Rome and the tyranny of the Catholic Church are more important historically than Malthus, since from the time of Clovis to the time of Malthus the amount of arable land increased arithmetically because there continued to be more land which could be exploited. I would argue that Caplan’s explaination makes much more sense than Malthus’ as for the past hundred years agriculture has grown not by increasing the acreage planted, but by technological advances in agriculture which only come from innovation due to increasing demand.
General Specific
Oct 9 2007 at 7:41pm
Caplan’s argument is extremely tenuous and wishful–one might say utopian. Marx would be proud.
It seems true enough that more people will produce more ideas, economies of scale, etc.–but Caplan has absolutely no quantative or substantial argument other than that. Redrawing a straight line as he does with figure 2.1 showing population and per capita both heading off to infinity has (a) no support in his arguments and (b) a profound argument against it–physical limits.
Why not draw a parabolic curve? Straight lines in economics almost always seem entirely misleading. Rhetorical slight of hand.
And the idea–as mentioned by some–that emergence negates malthus is not true–at least they make no arguments that it is true. It’s popular these days to use the idea of emergence and complexity as a way to avoid making a sound argument.
Caplan has no evidence that an increased population would have brought an earlier start to the industrial revolution. It’s just his unsubstantiated opinion which he enjoys because it furthers his need to avoid the possibility that there are limits in this universe and that the human animal, as tricky as it may be, might very well run up against those limits from time to time, in the past, and in the future.
Troy Camplin
Oct 9 2007 at 8:32pm
Emergence and complexity are not ways of avoiding making a sound argument — they are the reality of the world, something Malthus and other linear thinkers don’t understand. The fact is that production does not and has never grown at a linear rate — Malthus was wrong about that as he was wrong about the world in general — they, too, grow exponentially. The Green Revolution made our food supplies grow exponentially. New hybrids contributed to the continued exponential growth (it apparently never occured to Malthus that one could increase crop yields vertically, and not just by willing the plane of cropland). Genetic engineering will only speed up the process even more.
Malthus has been proven wrong time and time again throughout all of economic history — just like Marx has, just like all socialist ideologies have. When will we finally do away with Malthusian thinking? It should go the way of the dinosaurs, just like every other idea that has no real relationship to reality.
General Specific
Oct 10 2007 at 2:18am
“Emergence and complexity are not ways of avoiding making a sound argument — they are the reality of the world”
Please note I didn’t say the world isn’t emergent or complex. But the terms “emergence” and “complex” are often used to avoid actually talking about the details of an issue (they’re often a form of handwaving). That’s all.
“Malthus and other linear thinkers”
That’s exactly what Caplan is doing. A linear graph of population and per capita income. Going off to infinity.
“grow exponentially”
No systems grow exponentially forever. None. It defies physics.
Malthus’ ideas have to be tweaked. But they weren’t wrong. And it’s still not clear that they are wrong. The green revolution did change things–a combination of genetics or breeding combined with the use of fossil fuels.
But that doesn’t disprove malthus’ more general idea. It’s proven true for animals and–in the case of humans–we’ve possibly done nothing more than shifted and delayed.
Read closely Caplan’s argument: “These effects could easily suffice to overpower the Malthusian diminishing marginal returns effect
“Could easily suffice” is the important part. That’s called handwaving. Supposing. That’s all. It refutes nothing.
Matt
Oct 10 2007 at 12:03pm
One cannot dismiss Brian’s theory out of hand.
Implicit in the Malthus model is the idea that populations overshoot and undershoot the optimum population size, though Malthus only defined the bounds. After a plague, the economy would be underpopulated, so the apparent higher standard of living would diminish as the smaller popuation could not maintain assets efficiently.
The real technology yield is curved, with a peak at a population level that optimumly manages assets. The underlying intertia is a two force model balanced between tool making and baby making, the two forces being negatively correlated and clyclic. During the plague years, the cycles would be forced phased to the plague cycles.
What we need to know is what hapened after the plague problem was managed, in say 1700. Did that first generation focus on tool making (driven by longer outlook) or baby making (driven by population sizing).
General Specific
Oct 10 2007 at 12:31pm
“One cannot dismiss Brian’s theory out of hand.”
I don’t intend to dismiss Caplan’s critique entirely. But his arguments don’t overturn malthus, in my mind, in a general sense. Technology and ideas should be considered. Heck, emergence and complexity can be considered. But, and this is very important: the fact that ideas can be infinitely combined, that an infinite sentence can (theoretically) be created does not make the universe nor our interaction with it infinite.
Or to put it another way: The idea of Captain Kirk racing across the galaxy on the power of dilithium crystals does not lead directly or indirectly to real people racing across the galaxy.
A lot of people get confused about the difference.
Caplan should draw a real curve. One that takes into account resources available to humans, population, consumption, technology development. He can’t, because it’s too complicated. But just because something is complicated doesn’t make it infinite.
He can’t draw a curve that goes off to infinity to the right. There are limits. And once he admit that, by drawing the curve more accurately, he has to start considering them, because people will see that the curve doesn’t go off to infinity.
But he doesn’t want to have that conversation.
Both curves are wrong. Arguing against a wrong curve with another wrong curve is–wrong.
Troy Camplin
Oct 10 2007 at 2:41pm
The laws of phsyics are laws that constrain the emergent system of chemistry, and the laws of chemistry are laws that constrain the emergent system of biology. Living things all grow at an exponential rate. That is one of the laws of biological organisms that emerge. It, then, acts as a constraint on all those things that emerge out of the interactions of biological organisms. This includes farming and economy. Whatever linearity there may be in the world (and that little is found only in extremely simple Newtonian systems) has nothing to do with biolgical systems or any systems that derive from their interactions. There is no such thing as linear growth in biological systems or any system derived from biological systems. Any appearance of linearity has inevitably meant we have simply looked too far down the curve. Until we acknowledge that linear growth is not an option when discussing biological growth, or the growth of any system derived from biological organisms, we cannot actually understand the system in question, meaning we cannot have any kind of meaningful discussion about them, since any such discussion will be based on false premises.
In other words, if Malthus’ ideas require any sort of linear growth of any kind of system other than balls rolling down planes, then his ideas are deeply, fundamentally wrong.
The argument that exponential growth cannot be maintained is itself an argument outside of Malthus’ argument, since he is arguing for linear growth of food products. Since it has been shown that food production is not linear, his ideas are wrong. We have a different kind of argument if both population and food production are growing at an exponential rate. We can then discuss issues of the maintenance of exponential growth, etc. But other than posing the question of the relationship between food production and population growth, Malthus is completely outside any sort of discussion of these issues, since his premise is so completely wrong.
General Specific
Oct 10 2007 at 3:29pm
Troy: The three body problem, classic Newtonian physics, has chaotic solutions. It’s never been solved in closed form. All this talk about the newtonian world versus emergence and linearity versus non-linearity takes us from the essence of what I’m saying:
The essence of malthus, to me, is the relationship between production and consumption, with production reliant on a physical input–matter and energy.
When it came to humans, malthus was mistaken. Food supply, for example, could grow in ways he had never considered. He also never considered the significant amount of energy available in fossil fuels and the fertilization possibilities derived from fossil fuels as well.
But there is a relationship between production and consumption, and a technological relationship between productivity and resources. The question is whether production can keep up with consumption. In the past, it didn’t, so consumption (per capita) decreased as population rose. For animals, it’s always been that way. Matters changed significantly with the industrial revolution, but we simply don’t know how much.
Odds are that limits still exist. Humans are likely limited to this planet–interplanetary space travel is extremely unlikely–so most humans are fixed to this world. The resources on this planet are fixed and the energy flow from the sun also fixed. Fossil fuels are fixed and probably will be in production decline very soon–if not happening already. Other sources of energy–e.g. uranium–are also fixed.
So now it’s just a question of what the relationship in the future is between resources, production, and consumption.
Caplan has not demonstrated at all that production can keep up with his infinite number of consumers (in his chart) and therefore I’ll go with the physics of limits–his chart must curve downward in a malthusean sense after the population gets to a certain level.
Utopians with dilithium crystal power gallactic space craft can think otherwise. 🙂
TGGP
Oct 10 2007 at 4:01pm
General Specific, Malthus is just plain wrong for the current time period. That’s why Julian Simon made a fool out of Ehrlich. Malthus says that higher wages will be eaten up by higher population growth. What we observe now is lower birth rates among the wealthy and an epidemic of obesity among the lower classes. We are living in post-Malthusian times.
Matt
Oct 10 2007 at 4:07pm
Getting at the propermeasurement, IMHO.
First is simply extending Malthus to a complex, instead of real valued kernel. We can get a much better estimate in spite of the complexity. Malthus is a simple, real two function form of the general complex valued eigenvalue model of populations.
Extending malthus to the complex plane gets us a framework to handle general exponential growth, decay and cyclic markets.
This linear extension does not answer the debate on hand, because what we are talking about are quantum effects, that is, how did economies rearrange themselves when post-plague markets functioned quite differently than pre-plague markets.
To really get past Malthus here, we need to look very closely at 1700-1750 the emergence of long term capital markets, extension of banking, fertility rates, and wealth-census data. We need to reconstruct markets, as they existed and evolved over that time. In other words, go look at Clarks’s data, which I have not, and reconstruct changes in wealth distribution over time to determine which forcing function was the differential driver (outlook or population).
Clark seems to imply the forcing function was population sizing among sucessful groups, during plague years? What did he observe just between 1700 and 1750? I should read the book.
By the way, outlook is a measure of the ability to hold a price over time, and population size is the ability to commit to a transaction over a price range. This kind of research needs the concept of market inertia (or capacity) so that it has the start of a quantum framework at least.
Troy Camplin
Oct 10 2007 at 7:47pm
I don’t know what the three body problem and chaotics have to do with complexity and emergence, but what I was saying is that Malthus was looking at the world as a simple, linear system, whereas the world is, in fact, a complex, nonlinear system with emergent features. My argument is that his understanding of the world was wrong, so we cannot trust his conclusions. As has been pointed out, if you want to make some money, bet against anything a Malthusian says will happen.
General Specific
Oct 10 2007 at 9:20pm
” That’s why Julian Simon made a fool out of Ehrlich.”
I think Ehrlich was foolish to make such a bet when he didn’t have appropriate models on which to make his bet. But then again, that bet is way way over-discussed. It is largely meaningless.
The George Guilder’s and Julian Simons of the world are like broken clocks. Sometimes right, sometimes wrong, but largely evangelists.
“As has been pointed out, if you want to make some money, bet against anything a Malthusian says will happen. ”
I think it’s a matter of looking at the facts of the matter, not whether a malthusian is saying something or not. Models five years ago increasingly showed oil production peaking, and they’ve proven reasonably accurate–those who followed the geologists and not economists (who continually argued that oil will be below $20 a barrel) made money.
Malthus had an insight that I find insightful, wrong on some details, but all the same one that should be considered.
Troy Camplin
Oct 10 2007 at 10:12pm
When we look at prices adjusted for inflation, as we do in the following chart: http://www.inflationdata.com/inflation/images/charts/Oil/Inflation_Adj_Oil_Prices_Chart.htm
I don’t see any correlation between the price of oil and the existence of oil reserves. I do see the price of oil changing based on political decisions, including wars in the Middle East. Truth be told, if it hadn’t been for the latest war, do we know what the price of oil would be? In fact, if you look carefully, you can see the price of oil dropping throughout time when the U.S. government wasn’t doing something to drive prices up.
General Specific
Oct 11 2007 at 10:00am
Troy: There are two or three historical periods to consider.
(1) US production peaks (around 1970). Not because of environmental regulation. Because of geology. That then allowed OPEC to seize the initiative and price oil at a level they wanted. You might call that political, but the political was driven by US depletion–geological.
(2) All the production crises since that time were balanced out by Saudi ramp-up in production when necessary–and they were willing. So the price of oil was driven by the Saudi ability to wipe out any speculators if they so desired.
(3) Today. Saudis no longer have excess production capacity. They are likely in or near decline, ramping up with significantly more drilling but it’s a race against depletion. So the war in Iraq, which took maybe 1-2 MBPD from Iraqi production (more or less) could not be balanced by the Saudis.
Right now, global oil production seems to be at a plateau. Odds are demand will run up against production constraints in the next year or so.
Read the oil drum or econbrowser to get the latest information on this topic. Libertarian economists and thinkers have been predicting $20 oil for over five years now. They’ve been wrong. They will very likely continue to be wrong. Odds are, we’re entering a new era.
Dr. Troy Camplin
Oct 11 2007 at 3:25pm
The reaction to the embargo was political. When Reagan took office, he let the American people react economically to the high oil prices, people used less oil, and the embargo was broken. Subsequently, oil prices dropped dramatically. The prices were dropping prior the Reagan taking office, but we also see another peek around 1981, followed by a dramatic drop in oil prices, almost down to the levels where, based on the trend up to 1972 (when Nixon’s Keynsean policies began to take hold). The price peaks again during the first Gulf War, and then drops down to where one would have predicted oil prices to be if, again, the trend had continued past 1972, prior to government interference. One wonders what law was passed to cause the price to go up after 1998, but it is clear that oil prices were tied first to 9-11 (prices dropped, then started going up after this date), and then to the second Gulf War. Equally interesting is the fact that oil prices dropped after the 2006 elections. Or are we to assume that more oil was suddenly discovered?
General Specific
Oct 11 2007 at 10:32pm
” One wonders what law was passed to cause the price to go up after 1998″
Most likely the law of depletion. It’s a natural law. Visit the oil drum to learn more about it. US oil production peak in 1970 or so due to geological reasons. The decline was reduced a bit by Alaska, but the decline had already started.
The world will likely soon be in decline.
Troy Camplin
Oct 12 2007 at 9:12am
Wow. No set of facts will get you off message, will it? No need to investigate alternative theories if your theory explains everything to your satisfaction. It turns out that about 1997-8 there was a push to make oil companies pay their unpaid royalties. Now, how do you suppose they paid for those royalties? Could it be through higher oil prices?
General Specific
Oct 12 2007 at 11:02am
Troy: I believe there a variety of explanations to oil prices through the years, including the ones you present. My perception is that you are unwilling to consider my story: depletion. I accept some of the stories you’ve presented. I’ve said that oil prices were political, at times. Economic, at times. Right now, I think we are looking at depletion.
I’ve been studying this topic for about ten years (I’m an energy investor) and my gut, based on all the analysis, is that we are facing depletion and it has significant ramifications. James Hamilton at econbrowser seems to be in the same boat.
That’s all. I’m not beholden to any particular story. But the depletion story is making more sense.
All I say is give it some consideration. Don’t just think that reaganomics and taxes and politics are the only thing going on here.
Troy Camplin
Oct 12 2007 at 3:39pm
I would be more than willing to believe in depletion if I could see a statistical analysis that elminated all political factors and showed that oil prices did indeed start to trend upwards once those price-raising factors were taken out of consideration.
I have said elsewhere that we will never run out of oil precisely because as oil becomes depleated, prices will rise, and alternatives will then develop that were too expaneisve to create before, due to low oil prices. We’re still not there yet. Otherwise there would be no need to subsidize research into alternatives.
I’m still not entirely convinced that we have depleated our oil reserves, though. We are beginning to deplete those that are easy to get to, but there are still deeper sources, not to mention huge amounts of oil shale that, when we figure out how to get the oil out of it, will provide a lot of oil for along time.
General Specific
Oct 13 2007 at 4:00pm
One of the problems with alternatives is that the prices upon which they are considered viable continue to go up as the price of oil goes up. This is easily predicted based upon EROEI but the people who shouted “$40 oil makes oil shale or tar sands highly profitable” never considered the inflationary nature of rising oil prices on the equipment and processes necessary to dig out the sand and shale and to extract useful product.
Oil sands are profitable but even now the costs are accelerating dramatically. It’s a major problem. Check it out.
Shale is a dead end right now, and probably will be. There’s simply not enough energy returned on energy invested.
Coal liquifaction has potential.
Prices will go up. That’s is true. But depletion and higher prices do not mean that alternatives will pop up out of the blue. The volumes of alternatives cannot match poking a hole in the ground in Saudi Arabia or Texas, followed by oil under pressure gushing into the air. Those days are over.
Comments are closed.