A sizable literature on the education premium finds solid evidence of a “sheepskin effect“: diploma years pay noticeably more than other years. When I noticed that the General Social Survey has a DEGREE variable, I saw a golden opportunity to double check the robustness of the result.
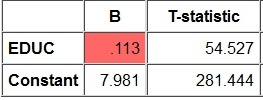
As a benchmark, I started by just regressing log earnings (REALRINC) on years of education. The result:
Next, I added DEGREE to the explanatory variables. Degree=0 if you don’t have a high school diploma, =1 if you have only a high school diploma, =2 if you have an associate degree, =3 if you have a bachelor’s degree, and =4 if you have a graduate degree. Result:
Once you control for degrees, every year of education raises earnings not by 11.3%, but by a mere 2.4%. Every degree, in contrast, boosts earnings by a full 25.6%.
To be sure, this set-up implicitly assumes that every step up the degree ladder is equally valuable. What if you relax that assumption? I defined HIGHSCHOOL=1 if you have a high school degree or more, JUNIORCOLLEGE=1 if you have an associate’s degree, BACHELORS=1 if you have a four-year degree, and ADVANCED=1 if you have a graduate degree. Here’s what you get:
In this more flexible set-up, a year of education is only worth 2.2% in extra earnings. But high school graduation gets you an extra 28.1%. Junior college gets you another 23% on top of that. A four-year degree gets you a 45.7% over high school. And an advanced degree gets you another 38.6% on top of a four-year degree.*
Qualitatively, this is just what you’d expect. Quantitatively, however, this result is far more extreme than any other sheepskin effect I can recall. The GSS is a huge, high-quality data set, so you can’t dismiss it as an aberration. The income data is admittedly subpar, because it’s derived from categorical data. But why would that sharply inflate the benefit of degrees relative to mere years of study?
If you’ve got ideas, please share – and show your work.
* For coefficients this large, there’s a modest approximation error – log points and percentage gains start to diverge. I ignore this fact for simplicity.

READER COMMENTS
Radford Neal
Feb 20 2013 at 9:08pm
I doubt that this demonstrates much. If everyone finished the degrees they started, there would be a perfect dependence between years of education and number of degrees, so it would be impossible to distinguish the “sheepskin effect” from a “years of education” effect. Since not everyone finishes, there are different effects to be estimated, but remember that each coefficient is for the effect given the other covariate.
As a result, if anything I’m surprised that the coefficient for years of education isn’t negative, when the degree variable is included. After all, who has lots of years of education but no degree? People who aren’t very bright, or aren’t very focused. Presumably this is more than compensated for by some people who actually do learn something useful from their education, even if they don’t get a degree, or by signalling effects of education without a degree, or by something else. I don’t think it’s possible to settle on an interpretation from just this data.
Jay
Feb 20 2013 at 9:14pm
What about the opportunity costs of each additional level of education (lost income, student debt)? How long does it take for that to level out?
Ben H.
Feb 20 2013 at 9:24pm
I agree with Radford Neal. I’d like to see how correlated DEGREE and EDUC are. Dividing effects between two highly correlated variables is very problematic.
genauer
Feb 20 2013 at 9:55pm
I think the remaining EDUC effect is in reality an age effect.
For people with engineering degrees, working in the private sector in Germany, income rose typically with age, by 2 % per year, until around 45, frontloaded.
In the public sector, the tariff tables were weaker, and more back loaded.
My impression from private industry in the US is similar.
Soo, you have to control for age and working years as well.
My understanding is also, that this age income rise flattens out much faster at lower education.
Otherwise, the size of the numbers is pretty much what I expected.
Milton Recht
Feb 20 2013 at 10:04pm
Each degree level includes some individuals who attended but failed to achieve a degree from a higher level.
Someone who goes to a four year college but fails to graduate at any level including after four years of college would be counted as a high school graduate.
Someone who goes to graduate school but is ABD is counted as a college grad.
While degrees have importance, the extra schooling at the next level beyond degree increases the sheepskin effect of the received diploma.
J. Goard
Feb 20 2013 at 11:53pm
It would be useful if we could separately examine fields where a certain degree largely serves as an artificial restriction of supply to increase labor price, particularly medicine and law for an advanced degree but also many public sector or officially credentialed private jobs for a 4-year degree.
genauer
Feb 21 2013 at 4:26am
What am I missing here?
According to my description Realrinc is family income in Dollars of 1986, or to multiply by 2.06 for 2013 Dollar.
if I try to convert the numbers here in yearly Dollar, I assume
ln( Realrinc ) = 7.821 + 12 (years) * 0.113
for a high school family, the most simple case
yearly present family income in 2013 = 2.06 * 9672
With a GM entry level worker getting something like 15$/hr * 2000 hours per year, ?
Do you divide by the number of wage earners per household, which would be closer to 2
Or what do I not see here?
RPLong
Feb 21 2013 at 7:45am
Further to Ben H., I think it might be useful to drop EDUC entirely and see what happens to R^2. I also agree that you should probably add an age variable to disambiguate EDUC from the mere passage of time.
It may also be interesting to compare people who have the same degree, but different values for EDUC, to see whether there is any premium derived from graduating early or spending additional time in school.
W W Brown
Feb 21 2013 at 9:07am
Presumably the educational degree ladder sorts people on the basis of intelligence, among other things, which is generally associated with higher earnings. Attributing the results to education may be comforting to educators, but without controlling for intelligence they shed little light on education’s true impact on earnings.
rvman
Feb 21 2013 at 11:48am
For clarity, if I am a data point, and I have an advanced degree, for me:
High School = 1
Junior College = 0
Bachelors = 1
Advanced = 1
Is this correct? This appears to be what you describe in the paragraph after the table, but I want to be sure I’m getting it right.
MingoV
Feb 21 2013 at 5:36pm
What I would like to see is a trade school effect and a certification/licensure effect. How much does a year of auto mechanics, appliance repair, dental hygienics, etc. add to income? What about becoming a certified electrician, plumber, computer repairer, etc.
I suspect that the effect of one year of trade school will exceed that of an Associates Degree.
Glen S. McGhee
Feb 22 2013 at 1:27pm
I, too, agree with Radford Neal.
In fact, the bang-for-the-buck degree is declining.
http://marginalrevolution.com/marginalrevolution/2013/02/average-earnings-of-young-college-graduates-are-still-falling.html
What more evidence for credential inflation do we need?
Comments are closed.