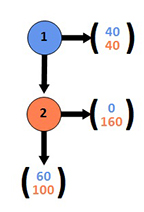
The last experiment in Humanomics is a variation of a treatment in an article by Mary Rigdon, Kevin McCabe, and Vernon Smith. In my version, people are paired to play the following extensive form game:
Person 1 makes the first decision by either ending the game or passing the play to Person 2. If Person 1 plays right, both people receive 40¢ that round. If Person 1 plays down, then Person 2 can either play right, yielding 0¢ for Person 1 and 160¢ for herself, or she can play down, yielding 60¢ for Person 1 and 100¢ for herself.
The students are told that “[t]his experiment will last for several rounds. Each round you are matched with a person in this room.” They are not told the exact number of rounds nor how they are matched. I have now run this experiment at least 100 times in classes and workshops and every time someone asks the question, “Are we matched with the same person each round?” To which I reply, “Each round you are matched with a person in this room.” Thinking that I did not understand the question, the student inevitably repeats it and I pertinaciously recite back the line from the instructions. After a couple exchanges of this sort, the students conclude that I am not going to tell them how they are matched. The point of the experiment is that the matching algorithm is unstated.* I want the students to know that they are matched with a person and not a computer robot. The question is what do they do when there is some doubt as to who they are encountering each round.
The experiment lasts for 20 rounds. Here are the results for the two sections:
Roughly 95% of the sessions that I have conducted look like section 2 by the end of the experiment. They also track quite closely what Rigdon et al. find with slightly different payoffs for the last 5 rounds: 47% of Person 1‘s end the game, 44% of pairs end up at the equivalent of the (60,100) outcome, and 9% of the pairs end up at the equivalent of the (0,160) outcome. Never before have I seen a session like section 1.
My first question after displaying the results is, “How do you think you were matched?” Half of the people report that they must have been matched with the same person each round. Both people repeatedly played down. It is not uncommon for a pair to be unknowingly matched with the same person each round and achieve the (60,100) outcome reach round. The other half of the Person 1‘s are unsure. They say they played down a few times, got burned more often than not, gave up trying, and are not quite sure about how they were matched. Their corresponding Person 2‘s are noticeably quiet. I wonder why.
Then I reveal the matching algorithm. The software counts how many times over the previous 5 rounds each Person 1 and Person 2 played down, ranks them from highest to lowest, and then matches them by rank in the current round. In the baseline treatment in Rigdon et al., which I did not conduct, the participants are randomly matched each round. When randomly matched, Person 1‘s who play down are likely to encounter Person 2‘s who play right so that by the end of the experiment 73% of the Person 1‘s end the game. Only 14% of the pairs reach the equivalent of the (60,100) outcome.
In Humanomics, we conduct this experiment before we read and discuss chapters 4 and 7-9 of Deirdre McCloskey’s The Bourgeois Virtues. McCloskey argues that something more than material payoffs is necessary to make commerce work. Even though we may not see it, she argues that the bourgeoisie practice the virtue of love in commerce. Not eros, obviously, but a sense of solidarity in the form of a trust that transcends material payoffs.
Why is it that Person 1‘s who play down expect that Person 2‘s will do the same? And why are they vocally disappointed, if not indignant, in the debriefing when Person 2‘s do not? Person 1 does not expect Person 2 to do as she pleases but to exercise her personal judgment and act as she must, as one does in a personal interaction with another human being. When another person is involved, the situation is not a solipsistic game against nature. Sure, payoffs matter, but they do not matter to the exclusion of the consideration that another person is involved. A sense of we transcends the pecuniary calculation when a positive sum gain is on the line.
When Person 2 plays down, it is because in some small way she cares about Person 1. That kind of love for another person is the point of the (60, 100) outcome, and it is what a Person 1 is looking for in a Person 2.
*Please note that I am not deceiving the students. I am not misleading by false appearance or statement. I am simply leaving it open to the students to infer how they are encountering each other.

READER COMMENTS
EclectEcon
Dec 3 2013 at 1:53pm
My experience with similar type games is that economics students and business students often try to show how hard-nosed they can be and how they can win in any situation. Meanwhile, arts and humanities students tend to behave as if they are saying, “yeah, whatever. Let’s share.”
I’d guess that section one had more arts and humanities students, where section two had more business students.
MingoV
Dec 3 2013 at 5:52pm
That’s quite a stretch of the meaning of love. There are two “non-love” reasons for Player 2s to play down. The first reason is that the experiment has no basis in reality, so Player 2 loses nothing real by not choosing right. If each player had to contribute $80 to participate, the outcomes would be much different. The second reason is the (incorrect) expectation of a prisoners’ dilemma-type situation. If every player knew how other players responded in previous rounds, then the down-down choice yields maximal payoffs for all. That wasn’t the case in these experiments, but, because of the unknown pairing algorithm, I don’t believe the participants realized that.
Tracy W
Dec 4 2013 at 4:56am
If people are ranked and matched based on their choices in the first five games are they initially matched at random for the first five games?
And don’t person 1s want person 2s to play down so the person 1s get 20 more? I really don’t see how trust transcends material payoffs here. The material payoffs seem obvious.
Bart
Dec 4 2013 at 2:22pm
@Tracy W
The first period is random and then the ranking gradually accumulates 5 periods in an average until it becomes a moving average.
Go back to the question, “Why is it that Person 1’s who play down expect that Person 2’s will do the same?” Yes, Person 1 is seeking a higher payoff, but what makes receiving more money possible or even a reasonable expectation?
Tracy W
Dec 5 2013 at 1:49am
@Bart – thanks for answering.
Based on your results in section two, playing down is a reasonable strategy as it results in more nearly half the time.
I recall helping one of my lecturers with a multi-round prisoners’ dilemma with anonymity and changing partners all the time. So no reputation benefits. The cooperation rates dropped throughout.
SaveyourSelf
Dec 5 2013 at 11:37pm
Bart wrote, “…what makes receiving more money possible or even a reasonable expectation?”
SaveyourSelf
Dec 5 2013 at 11:42pm
One item I find interesting about the setup of this game is that it bears some of the features of the prisoners dilemma but not all of them. In each round, Monopoly power is awarded first to Player 1, then to Player 2 if Player 1 passes. By keeping each player blind to who he is matched with, there is a temptation to use the monopoly power for self enrichment without personal cost. But there are several rounds, which encourages would-be monopolists to make friends, not enemies, so as to make out better in future rounds. The US Congress is set up in a very similar manner.
The most amazing part of the prisoners dilemma [and your game] is how glaringly it reveals the truly short-term extent of human thinking. Literally the people are separated from the group for mere minutes, yet they behave as though the new environment is the only one they have ever known. If humans were long term thinkers, we would predict “Section 1” outcomes most of the time. The fact that 95% of Bart’s outcomes matched “Section 2” and “only 14%…reach the equivalent of the (60,100) outcome” under random matching is staggering. The immediacy of the change in behavior is breathtaking. They act–in this game and in the custody of the police–as though they never had a relationship before the separation and never will again. The transience [or “adaptability” if your a cup half full kind of person] of human behavior is remarkable and humbling–as is the ever-present danger that monopoly power presents in the hands of a short term thinkers compared to the alternative.
Jed Trott
Dec 6 2013 at 1:47pm
For an experiment of this type I wonder what would happen if the scale was different. For instance if instead of 40 cents the base for each round was $40,000 or $4 million. I have to wonder about the ability to extrapolate anything from a game like this in which stakes are so low.
Comments are closed.