Saturos directed me to a comment by Eliezer Yudkowsky:
Just realized today that besides giving a real-world example of epistemic efficiency, markets also provide a real-world source of Newcomblike problems. Efficient markets can be so good at predicting you that if you raise rates today, that may cause a market reaction several years earlier.
He is referring to a paradox described as follows in Wikipedia:
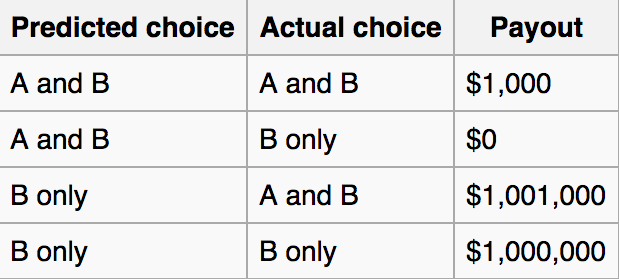
A person is playing a game operated by the Predictor, an entity presented as somehow being exceptionally skilled at predicting people’s actions. The player of the game is presented with two boxes, one transparent (labeled A) and the other opaque (labeled B). The player is permitted to take the contents of both boxes, or just the opaque box B. Box A contains a visible $1,000. The contents of box B, however, are determined as follows: At some point before the start of the game, the Predictor makes a prediction as to whether the player of the game will take just box B, or both boxes. If the Predictor predicts that both boxes will be taken, then box B will contain nothing. If the Predictor predicts that only box B will be taken, then box B will contain $1,000,000.
Nozick also stipulates that if the Predictor predicts that the player will choose randomly, then box B will contain nothing.
By the time the game begins, and the player is called upon to choose which boxes to take, the prediction has already been made, and the contents of box B have already been determined. That is, box B contains either $0 or $1,000,000 before the game begins, and once the game begins even the Predictor is powerless to change the contents of the boxes. Before the game begins, the player is aware of all the rules of the game, including the two possible contents of box B, the fact that its contents are based on the Predictor’s prediction, and knowledge of the Predictor’s infallibility. The only information withheld from the player is what prediction the Predictor made, and thus what the contents of box B are.
The problem is called a paradox because two analyses that both sound intuitively logical give conflicting answers to the question of what choice maximizes the player’s payout.
At the risk of making a fool of myself, I will now resolve the Newcomb paradox. If the predictor is an extremely skilled psychologist, who is 99.999% accurate in forecasting, then you should definitely chose box A + B, since your choice doesn’t affect the amount of money in box B. If the predictor is 100% accurate, then you should just choose box B, because the act of choosing box B causes, and I emphasizes causes, the earlier prediction that you will pick box B.
That second case might bother some people, but if you think about it your annoyance with the idea of causation going back in time is actually irritation with the concept of a perfect predictor. Something most people believe is impossible. But if one did exist . . . think about it.
OK, even if you think what I just wrote is nonsense, the application to markets and monetary policy is interesting. I’ve frequently talked about “long and variable leads” in monetary policy. This was a play on the “long and variable lags” claimed by Milton Friedman, who thought that changes in the money supply had a peak impact perhaps 18 months later. I claim that changes in the money supply affect prices and output before they occur, at least in most cases. That’s because policy is at least partly forecastable, and hence (as Yudkowsky notes) asset markets (and the economy) should be impacted by expected future policy.
But here’s where things get interesting. Policymakers also care about markets, which leads to the Bernanke/Woodford circularity problem. Markets are intensely focused on every twitch in Janet Yellen’s face during Congressional testimony, and Janet Yellen is focused on what markets are doing, as an indication as to whether money is too tight. Markets are the “predictors”, and Yellen is like the person trying to win a million dollars, only in her case it’s a sound economy that is the goal (say 4% NGDP growth).
But of course the market predictor is far from perfect, and indeed is also responding to other shocks like corporate profitability, so even if it were perfect you’d need an NGDP futures market, not a stock market as a predictor. And yet it is also clear that it has some useful information. Which reminds me of this fascinating Financial Times story from a few weeks back:
“It is reasonable for investors to wonder whether Fed’s December rate hike was a policy error,” admits Bob Michele, chief investment officer of JPMorgan Asset Management. “Historically the Fed has raised rates because either growth or inflation was uncomfortably high. This time is different — growth is slow; wage growth is limited; deflation is being imported.”
Perhaps most of all, many investors now fret that they are operating without a safety net they had grown attached to during the post-financial crisis era.
Markets have been buffeted by powerful headwinds since 2008-09, ranging from predictable Middle East strife to the spectre of the disintegration of the European common currency. But central banks have been a constant source of comfort in hard times, suppressing interest rates and market volatility, thereby reinforcing the view among investors of a ‘central bank put’, or downside protection.
Such an assurance now appears less certain given the recent approach from central banks.
The Bank of Japan has failed to expand its quantitative easing programme as expected; the European Central Bank dashed unrealistically high hopes of more eurozone QE in December; the People’s Bank of China has failed to calm concerns over China through aggressive action; and the Fed has started tightening monetary policy.As a result, the “era of asset price reflation, fuelled by both post-crisis undervaluation and aggressive central bank easing, is over”, according to Jeffrey Knight, global head of asset allocation at Columbia Threadneedle.
“It was fun while it lasted, as the recovery of financial asset prices from the nadir of the great financial crisis has been dramatic, one of history’s most fruitful periods for investors. But 2015 returns were rather different, and the early experiences of 2016 only reinforce the likelihood of a new investment climate,” he wrote in a note.
Indeed, Stephen Jen, a hedge fund manager, argues that this year’s sudden bout of concern over China has merely been the trigger for a broader reappraisal of central banking puts and omniscience by investors.
“My guess is that the new strike prices for these central bank puts are probably 10 to 20 per cent below where the markets are now,” he recently told clients. “It is the presence of this ‘air pocket’ that was the main trigger for the equity sell-off at the start of the year, in my humble opinion.”
The danger is that turbulent financial markets become a self-fulfilling prophecy by undermining confidence and weakening the global economy. That could trigger a feedback loop where turmoil hurts growth, which in turn fuels more choppiness.
Most economists maintain the risk of a US recession this year are slim, but markets are now pricing roughly even odds of one, and that in itself has consequences. . . .
Should financial turbulence infect the real economy, the US central bank’s plan to raise rates another four times this year becomes extremely challenging. Investors have long doubted this rate path, but now they are virtually laughing at it.
It may seem like market crashes cause a weaker economy, but in fact it is more likely that they predict it. Markets that crash are essentially predicting Fed failure. To make things even more complicated, the Fed uses market information in an attempt to avoid failure. A week before the FT article cited above, I wrote the following:
. . . the Fed knows that equity markets (and bond markets and commodity markets) often provide the first clue of an economy that is about to tank. Not a particularly reliable clue—recall the famous joke about the stock market predicting 11 of the past 6 recessions, but nonetheless an important clue.
Obviously the Fed can’t respond to each up and down in the market, nor should it. But here’s the problem. Because the Fed must pretend to ignore the stock market, it can’t act to correct a mistake until the carnage on Wall Street is so unmistakable that even average people think it’s necessary to step in. By that time it may be too late, a recession may already be underway.
When the FT talks about “air pockets” they are essentially talking about the extent to which central banks are willing to write off market warnings as “noise”. Beyond that point you have the famous central bank “put”. Ot at least they try to exercise a put; in 2008 they obviously failed. Fed policy seems like a stock market to monomaniacal Wall Street types, who confuse the markets with the macroeconomy. But Fed policy is actually a NGDP put exercised very clumsily by looking at noisy stock data.
The markets don’t know exactly where the central bank has set their put, so prices plunge lower and lower until they see signs from the central bank that it will boost NGDP growth. What looks like a stock crash causing an NGDP slowdown, is actually a stock market predicting that central bank passivity will fail to stop an NGDP slowdown. Markets also know that central banks prefer fed funds targeting to QE and negative IOR. And they know that central banks are “only human” and don’t like to admit mistakes by suddenly reversing course. That’s what caused the recession in 1937, and if there is one this year (still far from certain) that stubbornness will again be the cause.
The thing that has always frightened me about asset market plunges is that they already incorporate the Fed’s expected response. That should be as frightening to the Fed as the Newcomb Paradox game player contemplating the predictor’s uncanny predictive ability. You don’t just need to act; you need to do more than the market expected. Obviously that’s hard to do consistently, which means ideally you don’t want to allow NGDP expectations to plunge in the first place. In other words, “If I was headed for 4% NGDP growth, I wouldn’t start from here”.
The solution is for central banks to set up policy regimes that cause “The Predictors” to consistently predict success, i.e. to predict steady NGDP growth at 4% or 5% or whatever is the target. Did I mention NGDP futures markets?
PS. This post also relates to Paul Krugman’s famous “promise to be irresponsible” monetary stimulus at the zero bound. This idea is to promise to do something in the future that will cause the markets and the economy to behave better today. It’s called “irresponsible” because when the future actually arrives you may not want to honor that promise (economists call this ‘time inconsistency’), but if you have made it, then fear of losing your reputation leads you to honor it. Thus before Newcomb’s game begins you could promise to the predictor that you’d predict box B only. The idea is that $1,000,000 plus a good reputation for honesty is worth more than $1,001,000 and a reputation for dishonesty.
PPS. I’m in way over my head here, but doesn’t Calvinist predestination imply that by choosing to be good you cause (many decades earlier) God to select you as one of the chosen few to go to Heaven? It’s hard for me to wrap my mind around the idea that little old me could change God’s mind, but then I’m a fatalist that doesn’t believe in free will, so I guess I’ll just continue occasionally being bad. (But only in TheMoneyIllusion comment section, not this one.)
PPPS. Eliezer Yudkowsky has a wonderful introduction to market monetarist ideas, over at Facebook.
HT: Don Geddis

READER COMMENTS
Ben H.
Feb 14 2016 at 11:13am
A very interesting post. I won’t attempt to comment on the economics, but regarding the Newcomb paradox, reading a bit further in Wikipedia gives this:
“The exact nature of the Predictor varies between retellings of the paradox. Some assume that the character always has a reputation for being completely infallible and incapable of error; others assume that the predictor has a very low error rate. The Predictor can be presented as a psychic, a superintelligent alien, a deity, a brain-scanning computer, etc. However, the original discussion by Nozick says only that the Predictor’s predictions are “almost certainly” correct, and also specifies that “what you actually decide to do is not part of the explanation of why he made the prediction he made”.”
So the original formulation of the paradox appears to specifically rule out the sort of reverse causality you posit. I’m not sure what that does to your analysis. :->
Scott Sumner
Feb 14 2016 at 11:23am
Ben, Good point, but since there seem to be several versions I thought I would cover all the bases. It’s odd that people found this such a difficult puzzle in the case of the predictor being only usually correct; it’s a simple problem.
Njnnja
Feb 14 2016 at 12:12pm
While you are correct that actual causation is an important point to make (which is why it’s important to state the assumed theory of causation for different formulations of the paradox), your math is wrong.
When you say 99.999% accuracy, I am assuming that you mean P(Pred = A+B|Act = A+B) = 99.999% and P(Pred = B|Act = B) = 99.999%. If so, then E(payoff|Actual = A+B) = 99.999% * 1000 + (0.001%) * (1,001,000) = 999.99 + 10.01 = 1010
E(payoff|Actual = B) = 0 * (.001%) + (1,000,000)* 99.999% = 999,990.
So it is best to pick Actual = B when the accuracy is that high. In fact, even for levels of accuracy barely above 50% (pure guessing) Actual = B turns out to be the right choice (left as an exercise for the reader). The key thing to note is that if you make the game theory decision diagram, if you assume that there is a correlation between player actor and player predictor, you can’t use the typical “dominance” argument of decision theory with just 4 boxes.
Alexander Hudson
Feb 14 2016 at 12:13pm
I understand why the “promise to be irresponsible” phrasing that Krugman used many years ago was an intellectually appealing way to frame promises about future policy. But I think this framing has a downside. It reinforces people’s belief that higher inflation is always a bad thing, and that it is only to be tolerated as a necessary evil. Is it really all that surprising that central bankers, many of whom were shaped by the experience of the 1970s, are reluctant to adopt a policy that it’s own supporters call irresponsible? There’s nothing irresponsible about keeping nominal growth expectations on a stable trajectory. What *is* irresponsible is the Fed’s lack of commitment to the target it has set for itself, especially when it claims to have the tools to achieve it (though Yellen’s uncertainty about the legality of negative IOR is arguably a move in the opposite direction).
Brian Donohue
Feb 14 2016 at 12:14pm
Good post. The Yudkowsky thing is great.
Anonymous
Feb 14 2016 at 1:00pm
I think the key insight with the Newcomb’s problem thing is that which choice you make affects which boxes you’re offered. It is always better to take two boxes than one – it can’t not be. But if you’re someone who will take both boxes, you will never be offered an opaque box containing money. Your choice affects the situation you’re presented with as well as just the number of boxes you take.
This maps onto the correct choices in the Prisoner’s Dilemma: defect in a one shot, where your opponent cannot take your decision into account, try to establish cooperation in an iterated, where your behavior can and will be taken into account by your opponent when they make their decisions.
Kevin Dick
Feb 14 2016 at 1:23pm
I think your solution to the NP is funny given your focus on targeting the forecast.
It seems to me that the parallel solution to NGDPLT for the NP is to send out all the signals that you will one-box. Just like the best way to achieve the target NGDP is to send out all the signals that you will do whatever it takes to hit the target.
Of course, once the accuracy of the Predictor reaches some threshold, it’s just easier to become a one-boxer than keep track of all the signals you need to send. Just like the easiest thing in monetary policy is to actually be willing to do whatever it takes.
Scott Sumner
Feb 14 2016 at 1:37pm
Njnnja, I disagree, because your decision (by assumption) has no impact on whether there is money in box B.
(I think you need more than a correlation, you need a causal relationship, from picking back to prediction. If that exists, then yes you’d just pick box B. But in that case there’d be no choice to make, as you’d be “locked in” at that point. So there’s no “should” to be considered.)
Alexander, Yes, I’ve made that argument too.
Thanks Brian.
Kevin, Keep in mind that monetary policy is a repeat game, where credibility is important.
Tom Brown
Feb 14 2016 at 2:33pm
Scott, you might like this (from one of my favorite podcasts: “Rationally Speaking”), the topic being Newcomb’s paradox:
http://rationallyspeakingpodcast.org/show/rs140-kenny-easwaran-on-newcombs-paradox-and-the-tragedy-of.html
Hellestal
Feb 14 2016 at 3:55pm
Here’s Yudkowsky on Newcomb’s problem:
“First, foremost, fundamentally, above all else:
Rational agents should WIN.
Don’t mistake me, and think that I’m talking about the Hollywood Rationality stereotype that rationalists should be selfish or shortsighted. If your utility function has a term in it for others, then win their happiness. If your utility function has a term in it for a million years hence, then win the eon.
But at any rate, WIN. Don’t lose reasonably, WIN.”
I suggest reading the whole thing.
Njnnja
Feb 14 2016 at 4:22pm
The problem is that when you make the decision tree, you are breaking up the predictors actions by A+B vs only B, when the predictors actual actions are “be correct” vs “be incorrect.”
When you do that, the decision tree changes from:
Pred
A+B B only
A+B 1000 1,001,000
B only 0 1,000,000
Where A+B dominates B only regardless of what predictor chooses
to:
correct incorrect
A+B 1000 1,001,000
B only 1,000,000 0
Where now neither A+B nor B only dominates, so the actual prediction is dependent on whether you think the predictor will be correct or incorrect. I used a simple expectation because you presented the accuracy as a conditional probability. As long as you postulate that the predictor can do better than pure chance, the correct marginal axis is correct/not correct, rather than A+B/B only because the probability of the boxes are different in the two different rows.
marcus nunes
Feb 14 2016 at 4:34pm
A very short version of Eliezer Yudkowsky:
https://thefaintofheart.wordpress.com/2011/10/07/two-words-you-should-never-use-inflation-stimulus/
bill
Feb 14 2016 at 7:49pm
I guess the reason the stock market predicted 11 of the last 6 recessions is that the Fed paid attention the other 5 times. With a better Fed, the market would have predicted 11 of the last zero recessions. And with a Fed like that, the market would stop predicting recessions.
Kevin Dick
Feb 15 2016 at 12:06am
@Scott. I’m a game theory guy, so I’m sympathetic to your invoking repeated game dynamics. In fact, I used to hold your position on the NP.
However, Eliezer convinced me otherwise. So I’d urge you to reconsider. Hellestal’s link is a good place to start. Eliezer has come up with “timeless decision theory” to generalize his argument for one-boxing.
I don’t want to spoil the “aha moment” for you. But the key for me was to realize that most of our repeated game intuitions come from studying the Iterated Prisoner’s Dilemma. However, the IPL actually combines past reputation with possibility of future punishment. It also limits by assumption the reputational scope to past PD interactions with a single other player.
In contrast, the NP doesn’t include future punishment, but increases the scope of reputation to potentially all of your past behavior (depending on the formulation).
So the NP is essentially a game of _pure_ reputation. This changes the dynamics.
(Though Eliezer eventually argues that this means you should also cooperate in single-shot Prisoner’s Dilemma in all practical forms.)
ChrisA
Feb 15 2016 at 12:37am
I am not on Facebook so I can’t review the article, and in addition I am very new to the topic of Newcomb paradox, so probably my comment is a schoolboy error, but doesn’t the paradox simply disappear if the assumption is made that a “strong predictor” is actually impossible? It’s sort of like Maxwell’s demon, sure if it were possible then all sorts of paradox’s are possible, but we now know that (for reasons of information theory) a Maxwell’s demon is impossible, even a not very good one (a 50.1% accurate Maxell’s demon would have the same paradox). I don’t know if it can be proved in the same way, but I have a strong intuition that, without direct access to my thinking, even if they had an exact copy of my brain modeled, it would be impossible to accurately predict my reactions ahead of time due to chaos theory reasons.
Jose Romeu Robazzi
Feb 15 2016 at 7:12am
I think a promise to be irresponsible with inflation (“bad” because rising prices are bad) is a non-starter. But a promise to be irresponsible to with NGDP growth (“good” because it is growth) has a chance. People should switch paradigms fast …
BC
Feb 15 2016 at 7:51am
Scott: “Njnnja, I disagree, because your decision (by assumption) has no impact on whether there is money in box B.”
If I understand correctly what makes this a paradox, it’s that always picking B in turn requires that the Predictor predict B (to make the assumption that he is an accurate predictor true). The paradox seems to arise through the conflicting assumptions that your decision has no impact on whether there is money in Box B and the (near) infallibility of the Predictor.
This problem reminds me of the issue of concrete steppes vs. equilibrium, which Scott has written much about. There are no concrete steppes by which your decision affects the money in Box B. Yet, through the equilibrium condition that the Predictor make accurate predictions, your choice does impact the amount. There are no concrete steppes, but it’s a simultaneous system.
Scott Sumner
Feb 15 2016 at 9:37am
Everyone, It seems to me that the Newcomb’s Paradox game is in a sense under-described. We don’t know how the predictor predicts.
I suppose there are theories of prediction where you’d take box A + B. For instance, if he predicted based on his knowledge of your genetics.
In contrast, suppose that he was a mind-reader, and could read your mind if you mentally pre-committed somehow to pick box B. Then you’d want to try to mentally pre-commit to take box B. But in that case there is no “choice” at the moment of picking, because you’ve pre-committed. Thus if you were religious you might mentally tell yourself “Dear God, please send me to Hell if I pick boxes A +B.” And let’s assume the predictor can read your mind and know that you pre-committed. That would work.
My point is that the outcome depends on what you assume about the game. As I said before, if the predictor was 100% accurate then you’d always just pick B. But I still say that if he is predicting based on genetics, you’d pick A + B, and hope you were one of the rare exceptions.
Scott Sumner
Feb 15 2016 at 9:39am
BC, Keep in mind that monetary policy is a repeat game.
In that case you always take box B.
Njnnja
Feb 15 2016 at 11:47am
hope you were one of the rare exceptions.
The problem with this line of logic (well, it’s not really a problem, just the reason why you disagree with the paradox), is that your decision criteria is a maximax criteria. In that case, then yes, unless you are 100% certain that you never end up in boxes A+B/Bonly or Bonly/A+B, you will always prefer A+B. But maximax is not really a great way to make decisions, particularly when the difference between a low probability $1,001,000 and a high probability $1,000,000 is only $1,000.
I used expected value since that is the most straightforward criteria to use. And maybe it would be better to specify in the question, “choose A+B or Bonly to maximize your expected value.” Then merely picking A+B and hoping that you end up in the low probability A+B/Bonly box is more obviously a bad way to pick your row.
PS BC’s analogy to “concrete steppes” is quite apt. You don’t have to believe in any form of causality to choose box B only, all you need to do is believe that the probability of being in box A+B/A+B is greater than the probability of being in box A+B/Bonly if you choose A+B, and that the probability of being in box Bonly/Bonly is greater than the probability of being in box Bonly/A+B if you choose Bonly. Note that if you don’t believe that relationship between probabilities is possible then there is no paradox.
BC
Feb 15 2016 at 5:31pm
If one accepts Njnnja’s argument and picks B only, then Scott’s argument that one can do better by picking A+B is correct. A+B dominates B only for all Predictor’s choices.
However, if one picks A+B, then the Predictor will predict that with high probability. (Although the Player’s choice should not be random — that would make Box B contain nothing — the Predictor’s choice can be, and presumably should be, probabilistic. Otherwise, what does it mean for the Predictor to be 99.99% accurate? Accurate over what probability space?) So, one will do better (in expected value terms) with Njnna’s strategy.
Scott and Njnna’s arguments are both correct and both show that the other’s is incorrect. That’s why it’s a paradox. The Predictor can see into the future (perhaps with some error) yet, after the Predictor commits, the Player can make a different choice, but the Predictor can presumably anticipate that change,….
The Predictor’s clairvoyance changes the concept of time, causality, and committment. Time travel leads to all sorts of paradoxes, and the Predictor’s clairvoyance effectively allows him to travel through time.
Scott Sumner
Feb 16 2016 at 12:17am
Everyone, Suppose you pick A+B. Is there ever a case where you later regret this choice? Is there a scenario where the contents of the two boxes are revealed, and afterwards you go “oops, I should have just picked B”
ChrisA
Feb 16 2016 at 2:06am
If I was I asked to play the game I would delegate irrevocably my choice to a Robot, that could only provide the answer B, and then share the Robot programming with the Predictor. So the Predictor now must predict that I will chose B, and I will get $1m. The delegation must be provably irrevocable as otherwise the Predictor will predict I would override the Robot and choose A&B. Generalizing I would say that, unless you were able to prove commitment to the predictor ahead of time, you should always chose A&B. This I guess is the analogy to Monetary Policy – the commitment to NGDPLT must be mechanistic in nature and not subject to override by the man in charge.
Njnnja
Feb 16 2016 at 8:11am
Suppose you pick A+B. Is there ever a case where you later regret this choice? Is there a scenario where the contents of the two boxes are revealed, and afterwards you go “oops, I should have just picked B”
Let’s say that millions of people play the game. Plenty of them are going to pick A+B (probably because of the dominance argument, but the reasoning doesn’t really matter). Of those that actually pick A+B, how many did the predictor predict B only, and put $1,000,000 under box B?
If your answer is “lots of them,” then you aren’t in the world of Newcomb’s paradox. It is assumed that the predictor is a good predictor, so there should not be many people who select A+B and walk away with $1,001,000. In fact, the vast majority of those that select A+B should walk away with $1,000. That is assumed in the setup, and is a requirement just as important as not magically finding $2,000,000 under box A, or looking under a new box C.
On the other hand, of the millions of people who just chose box B, the vast majority of those people will walk home with $1,000,000. So imagine if you are observing all of this, and you picked A+B, but were not one of the very few lucky ones to get $1,001,000. You see all these people who picked box B walk away with $1,000,000. Really imagine yourself in that scenario, holding nothing but $1,000 and a broken model of how the game works, while watching those with a “wrong” model walking away with $1,000,000. I hope you would say “oops, I should have just picked B.”
Or even more strikingly, let’s say that go through all this, and you are given a chance to play one more time. Would you really still pick A+B? Your logic tells you to, but you just saw tons of people become millionaires by picking B only, while the people who agree with your model only have $1,000. People who were worried about hyperinflation at the dawn of QE were merely incorrect. People who worry about hyperinflation now are crazy. When reality doesn’t fit your model, do you change your model, or claim reality is wrong?
Of course this is all contingent on the predictor actually being a good predictor, and being able to have an a posteriori distribution of the type described in the setup. If you disagree that such a predictor could ever exist, then there is no paradox. If the predictor can never do better than guessing, then the math of choosing A+B holds, and in the above example, there are about as many people walking away with $1,001,000 from choosing box A+B as there are walking away with $1,000,000 from choosing box B, and if you are someone who picked A+B and only got $1,000, then there is no reason to believe that giving up box A would have given you any better chance of finding $1,000,000 in box B.
Note that this is different from the stock market predicting a recession and then the Fed correcting before it hits. In that case, the market can be a good predictor even though it’s prediction does not come to pass. But that is only because the Fed has the ability to see the market’s choice and change their own path, which is not an option in the NP game. In the NP game, it is assumed that you and the predictor make your choices without observing the others, in a one-step process.
jonathan
Feb 16 2016 at 8:43am
I’ve never quite understood the fascination with Newcomb’s problem. It’s just a simple dynamic game.
At time 1, the Predictor chooses whether or not to put the money in the boxes. At time 2, the chooser decides whether to take one or both boxes.
Clearly the solution with commitment is for the chooser to take the one box. But this isn’t a subgame perfect nash equilibrium — once the money is in the boxes, it’s better to take both.
So this just reduces to a question of commitment. It seems that this causes many people to go crazy, and invent convoluted stories about why it is correct to take the one box. My best guess is that these are commitment routines in the brain kicking in. Human psychology contains enough irrationality to enable some limited commitment, which clearly is useful in many social contexts.
Njnnja
Feb 16 2016 at 9:48am
It’s just a simple dynamic game.
The simple dynamic game that you propose is *not* Newcomb’s paradox. Let’s call it “jonathan’s game.” You are correct that jonathan’s game is quite straightforward to analyze. But there is nothing in jonathan’s game that makes the predictor a good predictor, which is one of the required assumptions in Newcomb’s paradox. Just because you and I don’t know what the predictor’s decision strategy is that leads to a posterior distribution assumed by Newcomb does not allow us to change that assumed distribution to something else. You can’t change the assumptions of a thought experiment and still say that you are analyzing the same problem.
Of course, that highlights exactly what Newcomb should be highlighting. If you don’t believe that any decision algorithm can generate the distribution assumed by Newcomb’s paradox (e.g. you don’t believe that human behavior is predictable, strong form theories of free will, etc etc etc), then you will say there is no paradox, and A+B is correct. But then you are simply refuting the assumptions of Newcomb’s paradox and arguing that, in reality, you will always play jonathan’s game, *not* saying that A+B is the correct choice in the hypothetical and potentially fantasy world described by the constraints and assumptions of Newcomb’s paradox.
jonathan
Feb 16 2016 at 11:25am
Njnnja:
You misunderstood what I am saying.
I am *not* saying that two-boxing is “correct”. Only that this is the solution to the analogous game without commitment.
If you can commit to one-boxing, then clearly this is the better course.
I am not denying the hypothetical. Besides, under the standard assumptions of game theory all players do perfectly predict others’ behavior.
Njnnja
Feb 16 2016 at 11:56am
@jonathan:
You are denying the hypothetical because your “predictor” has no predictive ability. It is merely a second player, the same as in any run of the mill decision theory problem. Newcomb’s predictor *is not* merely a second player that uses backward induction on the payoff matrix to figure out what you are going to do. So long as you think that is all that is happening, you will not understand Newcomb’s paradox.
under the standard assumptions of game theory all players do perfectly predict others’ behavior.
Your confusion comes from the fact that you don’t understand the difference between predicting the other player’s *behavior* versus predicting the other player’s *choice.* For example, in a typical decision theory problem, you can (and do) predict the other players unconditional behavior by analyzing their payoffs conditioned on your own choice. But a typical decision theory problem that does not have a single equilibrium may prescribe using a random strategy. In that case, player 1 may know that player 2’s best strategy is to select choice 1 30% of the time, and select choice 2 70% of the time. Player 1 will make a strategy based off perfect knowledge of player 2’s behavior, but not of player 2’s choice.
Although Newcomb specifically disallows random choice as a strategy, the difference between a predictor knowing your behavior versus knowing your choice is analogous. Your predictor knows the player “actual”‘s” *behavior*. Newcomb’s predictor knows the player “actual”‘s *choice*. Questions of commitment are irrelevant because all that matters is the actual player’s choice, and the fact that the predictor can, with great certainty, know actual’s choice.
k
Feb 21 2016 at 4:20am
The probability vs certainty criteria needn’t make a difference in deciding causation. For instance, say you have a perfect predictor P1, for whom you would only chose one box due to your ascribing causation. Now say one has P2 who follows P1 99% of time and decides randomly the rest. Your position that there is causation involved with respect to P1 shouldn’t change with P2 (it just becomes diluted by a tiny amount).
If there is some value in this intuition behind the criterion, maybe there is a better way to frame it.
Comments are closed.