Earlier this year, my Ancestry and Long-Run Growth Reading Club walked through Putterman and Weil’s “Post-1500 Population Flows and the Long-Run Determinants of Economic Growth and Inequality.” (Quarterly Journal of Economics, 2010) Quick review: Putterman and Weil measure the ancestral origins of the world’s current inhabitants, then show that past civilization of countries’ inhabitants is a much stronger predictor of current economic prosperity than past civilization of countries’ territory.
Instead of looking at the long-run effects of places’ traits, they look at the long-run effect of tribes’
traits. They focus on two measures: state history and years of
agriculture. State history measures how long a country “had a
supratribal government, the geographic scope of that government, and
whether that government was indigenous or by an outside power.”
Following previous work, they massage this measure: “The version used by
us, as in Chanda and Putterman (2005, 2007), considers state history
for the fifteen centuries to 1500, and discounts the past, reducing the
weight on each half century before 1451-1500 by an additional 5%.”
Years of agriculture, in contrast, is not massaged. It’s simply the
“the number of millennia since a country transitioned from hunting and
gathering to agriculture.”[…]
Now for the punchline: Migration-adjusted measures are much more
predictive of modern GDP than raw measures. “Not surprisingly, given
previous work, the tests suggest significant predictive power for the
unadjusted variables. However, for both measures of early development,
adjusting for migration produces a very large increase in explanatory
power. In the case of statehist, R2 goes from .06 to .22, whereas in the
case of agyears it goes from .08 to .24. The coefficients on the
measures of early development are also much larger using the adjusted
than the unadjusted values.”
The more I explored this paper, however, the more I realize that the world’s three most populous countries – China, India, and the United States – are big outliers. The people of China and India have great scores for state history and agriculture, but remain poor. The people of the United States have mediocre scores for state history and agriculture, but remain rich. If these three outliers were Grenada, Slovakia, and Botswana, I wouldn’t demur; outliers have ye always. But the fact that the three countries with the most people manifestly deviate from Putterman-Weil is troubling to say the least.
The obvious remedy, as my last post explained, is to run a weighted regression, to place heavier weight on more populous countries, and lighter weight on less populous countries. GMU econ prodigy Nathaniel Bechhofer volunteered to do all the legwork, and David Weil confirmed the accuracy of his output. Specifically, Bechhofer did the following for Putterman-Weil’s Table 4, columns (2) and (6).
1. Replicate the original results.
2. Re-do the original specifications with year-2000 population weights.*
You can access Bechhofer’s unabridged results here, here, and here. For now, though, let’s walk through the basic findings.
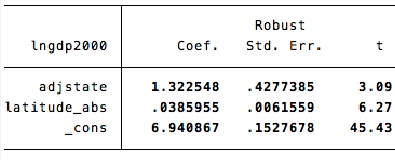
Putterman-Weil’s original output for the effect of ancestral state history and absolute latitude on modern per-capita GDP:
The same output, with countries weighted by population:
Putterman-Weil’s original output for the effect of ancestral agriculture and absolute latitude on modern per-capita GDP:
The same output, with countries weighted by population:
In both cases, the original coefficients imply huge positive effects of ancestral development on modern living standards. And in both cases, these huge coefficients actually turn negative after weighting for population. For agricultural history, a large statistically significant positive effect transmutes into a large statistically significant negative effect. Reviewing all of Bechhofer’s results, the signs on ancestral development are not uniformly negative, but Putterman-Weil’s dramatic positive results never re-emerge.
In stark contrast, the measured effects of sheer geography withstand population-weighting with ease. Absolute latitude continues to have a huge positive effect. So, to a slightly lesser extent, does being land-locked. (See the unabridged results).
What does this all mean? At minimum, the apparent effects of ancestral development on modern living standards are not robust. They don’t proverbially “leap out of the data”; they hinge on the debatable assumption that every country on Earth, no matter how small, is equally informative about the causes of economic development.
Personally, I’d go further: Despite its ubiquity in growth regressions, the equal-weighting assumption is silly. China, India, and the United States obviously teach us more about human societies than Grenada, Slovakia, or Botswana. And what they teach us is that ancestral greatness is not vital for modern prosperity.
* Bechhofer also tried year-1500 population weights, with very similar results.

READER COMMENTS
Martin Ljunge
Jun 23 2016 at 5:01am
Interesting. But why would linear population weights be “right”; it seems an extreme case. You kind of get a two point data set with China and India dominating most other data points.
How much do you need to weight population to changes the baseline results? Square root, cubic root, log, etc? What about assigning an arbitrary weight of 10, 20, or 50 to the countries deemed more important?
Thanks,
Martin
Michael
Jun 23 2016 at 7:53am
one problem is that (the aggregation of people int) countries are highly endogenous. Another is that the dynamics of (the growth of) those countries are obviously quite complicated, probably chaotic
What Putterman-Weil show is probably that if you want to create a successful new country, “who” matters more than “where”, at least as of today
What happens long-term is another matter. There seems to be a certain curse in empire-building, so you can create poverty from success
On the other hand, let China grow for another while, and it may well change sides from being a negative outlier to a success story
Also, haven’t read the paper, but how does the US turn out to be an outlier, if all immigrants are richer there than in their countries of origin? Must be a) some screwed-up weighing/averaging, or b) it’s the same as for China, there is some unrealised growth potential
In any case, varying the “now” of the estimates will probably also prove the results to be unstable. Why should 2016 be closer to some ideal equilibrium than, say, 1900?
Nathan W
Jun 23 2016 at 8:40am
Yesterday i was arguing that economic size might be a more relevant weight than population for comparing institutions (because it’s relevant to what’s presently influential in the world and thus how much attention we need to pay to it). But in the case of this study framework, it seems to me that population size should clearly be perceived as a more appropriate weighting of size than economic clout.
Considering that the 20th century saw such a flourishing of diverse new political systems, I still think there can be good value in exploring non-weighted comparisons as well, for a fair few purposes in political science.
brad
Jun 23 2016 at 9:47am
Also, haven’t read the paper, but how does the US turn out to be an outlier.
I believe the US is an outlier because of its success. The population of the US is mediocre when it comes to the measures Putterman and Weil look at but yet is one of the richest countries in the world.
randy
Jun 23 2016 at 11:12am
I haven’t read it either. My initial response is that unweighted might be more relevant after all. If growth is mostly a function of institutions plus culture, and institutions are country-specific, then you wouldn’t want China and India to drive the regression (as Martin pointed out). Instead, you want to see which sets of cultures/institutions drive growth. That’s unweighted.
Note that none of this makes any sense without a proper causal analysis… regressions only tell you conditional correlations.
gwern
Jun 23 2016 at 12:02pm
I agree that the results don’t really jump out, but I’m also not sure that either extreme of weighting really makes sense.
Why does one do weighting? Well, you do it, generally, to reflect sampling error: if you are running a census and you ask 10 people in 1 zip code about their income, and you ask 100 people in another zip code, you will want to weight ‘average income in zip code A and zip code B’ by the precisions; if you don’t, you’ll be amazed by how very low or very high some zip codes’ incomes are.
But in what sense do our national incomes or GDPs have this kind of sampling error? Barbados may be a small country, but surely its income is measured as accurately – if not more accurately – than a super-giant nation like China or India’s! All these country point estimates can be considered extremely precise. Their error all lies in systematic error, not random/sampling error. (Our estimates of Barbados GDP and China GDP are surely off by a lot, tens of percents, but that has to do with different government datasets, dishonesty in reporting, economic structural differences, etc, all things we can’t cure by calling up a random Barbadian or Chinese person and collecting another survey datapoint.)
On the other hand, per-country weighting feels implausible as well. Surely China tells us more than South Sudan? Not thousands of times more, of course, like in proportion to population sizes, but definitely more.
If we include population at all, for technical reasons, we might log-transform the population sizes or root them or something to get population size into a normal rather than skewed distribution as our statistical procedures demand, but that doesn’t tell us if we should be in the first place.
Here’s another analogy. We are interested in corporations and what makes them successful, and we collect data about a broad spectrum of American corporations from mom-and-pop shops to the giantest giants like Apple, Microsoft, Google, and Exxon, and we create covariates like industry, whether they sell to end-consumers or businesses, what sort of incentives they offer their staff (salary or stock options?), how they hire, how they promote, whether they use management consulting agencies, follow best-practices, what the ethnic breakdown of their staff is like, etc, in the hope of finding good predictors of corporate profitability which might even be causal.
We do all this and run our linear regression – weighted least squares, of course, by gross revenue, since it stands to reason that a company with billions in revenue has more to tell us than a little company with a few million in revenue – and what do we discover? That the only statistically-significant variables are whether a corporation makes smartphones, OSes, search engines, or drills oil, and offer stock options to employees. (Oh, the other variables all have point-values, of course, but the p-values are enormous because the available data for them is thousands or millions of times less precise than for the best variables.) We’ve learned something, but not necessarily what we wanted to.
I think the problem here is that population is not exogenous to income or success, however you want to define that. It is endogenous. A successful state expands, constantly. The original homeland of the Han is a tiny fraction of the territory and populations that China controls now. Even the biggest ancient Indian kingdoms don’t come close, AFAIK, to how big India is now. The USA started as a few colonies huddled on the East Coast. Japan also has expanded greatly historically (I’m reading the Man’yoshu now, and it’s clear from the warfare and place-names and frontier guards, that despite the heavy imperial propaganda and fawning, the pre-Heian empire was not strong or all that large, even excluding the Ainu territories.) It would make more sense to include population as an outcome in a multivariate regression, especially since some people consider larger populations to be as valuable as any wealth. Or perhaps move to stronger regression frameworks like SEM and look at models like ‘ancestry ~> population; population ~> wealth; ancestry ~> wealth’.
There’s also the issue of contemporary events causing residuals. North Korea will become much wealthier once it’s finally freed of its totalitarian dictatorship, just as China became much wealthier once the Communist Party got out of the way. If you had run this regression population-weighted 30 years ago, the results would have been different than they are now; while I suspect the unweighted regression would not be much different.
Comments are closed.