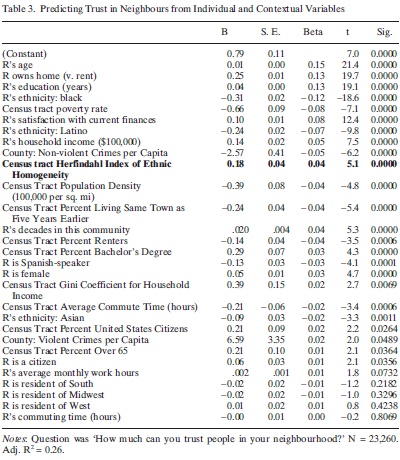
When Robert Putnam runs a proper statistical horserace, one of his favorite predictors of trust – diversity – barely matters. To recap:
Now a diversity skeptic could look at Putnam’s results and say: “Fine, diversity per se is no big deal. But Putnam does show that blacks and Hispanics have low trust. And that’s controlling for household income, the area’s poverty rate, and Spanish prevalence, all of which further depress trust. The presence of blacks and Hispanics is truly terrible.”
The easiest reply is: “You’re right qualitatively, but not quantitatively.” The whole point of a regression is to measure the size of effects, not just their directions – and the size of demographic effects is modest. Suppose the black share rises from 5% to 55%, the poverty rate rises from 10% to 40%, and average household income falls from $75k to $25k. This drastic demographic shift reduces Putnam’s predicted trust by .31*.50 + .66*.5 + .5*.14 = .56. Is that massive? No, because Putnam measures trust on a 4-point scale. .56 is less than 20% of size of the trust spectrum – noticeable, but hardly the end of the world.
But there’s a subtler reply. Namely: The effect of demographics on trust is zero-sum. If low-trust people move into a high-trust area, the change is bad for the incumbents but good for the entrants. Calling black migration “bad for trust” is just NIMBYism: keeping low trust away from you doesn’t make society’s trust higher.
Isn’t this always true? No. If, as in Putnam’s original story, diversity per se were really bad for growth, segregation would sharply raise average trust. Indeed, segregating two communities could conceivably raise trust in both communities. This is what makes diversity a special social variable. If diversity in and of itself has bad effects, so does integration – regardless of the characteristics of the mingling populations. If the effects of diversity are demographic effects in disguise, however, integration has distributional effects, but is zero-sum overall.
In a sense, then, Putnam was right to focus on diversity, because diversity is conceptually special. In the real world, arguments about diversity usually boil down to identity politics: Diversity is bad if it hurts my group, good if it helps my group. In theory, however, you could have an anti-diversity universalist – someone who thinks that society as a whole will be better off if people stick to their own kind. Putnam’s empirics suggest that anti-diversity universalists are rare for a reason: The numbers just don’t add up.

READER COMMENTS
JFA
Jun 19 2017 at 1:52pm
I wish economists/sociologists would stop running a linear regression on ordinal outcome variables. A 0.56 decrease on a 4 point-scale doesn’t mean anything because the scale is ordinal and saying such-and-such leads to a 0.56 decrease is treating it as cardinal. The reason why you can’t do that is because a trust level of 2 does not reflect twice as much trust as a trust level of 1.
Hazel Meade
Jun 19 2017 at 2:02pm
I think we should be curious as to what accounts for the low trust among black and Hispanics.
Do blacks and Hispanics have low trust in majority black or Hispanic countries? Do they have low trust only in black enclaves within majority white societies? Do they have low trust only in the Americas, or in Africa as well? Do they have low trust in mixed-race middle-income neighborhoods?
There are a lot of questions that are unanswered, which makes it impossible to say that low trust is an inherent personality trait or something induced by the social environment. I’m inclined to think that living within a society which is racially discriminatory is going to cause trust issues, and hence that high trust multi-racial societies are possible with appropriate social norms forbidding racial bias.
Emily
Jun 19 2017 at 2:55pm
/Is that massive? No, because Putnam measures trust on a 4-point scale. .56 is less than 20% of size of the trust spectrum – noticeable, but hardly the end of the world./
I don’t think that’s how you decide whether it’s massive or not. What are the actual, say, quartiles in terms of the trust distribution? What’s the score of a place we think of as being low-trust? High-trust? (I’m assuming it’s not adjusted to be uniform, I take this back if it is.)
Abe
Jun 19 2017 at 3:15pm
I agree with JFA. How is this at all warranted? An increase of 1 diversity corresponds to an increase of 0.56 trust? What does that mean? The difference between 2 trust and 2.56 trust is not the same as the difference between 1 trust and 1.56 trust, even if we grant the notion that 1, 1.56, 2, and 2.56 trust are notions that make any sense.
I’d honestly like to be corrected here. If economists or sociologists could come up with a justification for this sort of thing, I’m all ears.
Nathan Smith
Jun 19 2017 at 4:19pm
Wait a minute. Am I right in concluding that local inequality RAISES social trust?
The Census tract Gini coefficient for household income is 0.39. So if you went from perfect equality (Gini=0) to perfect inequality (Gini=1), people would become 0.39 more trusting, on a 4-point scale. Really?
If this is true, it seems like Putnam has another politically incorrect story to tell: trust is fostered by segregation and plutocracy.
Emily
Jun 19 2017 at 9:58pm
I don’t think the ordinal/cardinal issue is that big of a deal. Or, rather, it’s potentially the same big deal as if you had an actually continuous, more intuitive variable: there’s a potential non linear effect. Even if the variable were “what percent of your neighbors are trustworthy,” it could still be that a 10 pct increase means different things at different places on the distribution in terms of where the action is in predicting the thing we actually care about.
Abe
Jun 19 2017 at 10:46pm
Emily,
I’m not sure if we disagree or not. Let me be more explicit about the complaint. There are two random variables X and Y which are ordered set-valued, X being “trust”-valued, and Y being “diversity”-valued. We then map these ordered sets onto the real line in an order-preserving way to obtain random variables X’ and Y’, which we sample and run a linear regression against. But there is no reason to choose any particular order-preserving injection into the real line. We could have chosen any order-preserving injection we liked, and gotten a line of best fit with any slope we liked.
Of course, we could have run a least squares over a much larger class of functions than linear, and gotten a strange, non-linear relationship. I guess the point is that running a least squares against two variables which only carry an order structure is like running a least squares over a huge class of functions, and then pretending you ran a least squares over only lines.
Dangerman
Jun 20 2017 at 1:59pm
Oh boy, you really doubled-down on this one!
In general, I’m a firm believer that any argument in the form “yes, [in group], allowing [out group] to [do X] will make you worse off… but think of how it will make [outgroup] better off!” are always failures.
No one, and no group, is that altruistic.
An analogy…
One of the justifications for ending ability-grouping in primary education is that “mixing the dumb kids with the smart kids will, yes, make the smart kids slightly worse off… but it will make the dumb kids much better off!”
That’s great if you’re the parent of a dumb kid. If you’re the parent of a smart kid, not so much.
So, to further hammer the analogy… Prof. Caplan… why don’t you send your (clearly smart) kids to public school, where they can raise the *average* well being of the dumb kids?
(See, no one is that altruistic.)
Hazel Meade
Jun 20 2017 at 5:14pm
@Dangerman, what if there is a long term benefit of integrating the low-trust group, such as raising the trust levels of the low-trust group through the transmission of the high trust group’s social norms?
If we could predict that net trust would decrease in the short term, but eventually increase back to or higher than the same level as the high trust group, wouldn’t the high trust group ultimately be better off?
Dangerman
Jun 20 2017 at 5:25pm
@Hazel – sure, that’s a perfectly reasonably hypothetical.
But does it actually exist?
David
Jun 21 2017 at 10:37am
I’m noting a few things:
1. No interaction terms, unless I’m missing something
2. No model selection apparent since the lower significance values are > 0.2.
Converting ordinal to continuous for regressions is a decent first pass, but there are better ways of handling ordinal outcome variables.
gda
Jun 25 2017 at 7:40pm
It would seem that it is not only the climate scientists who are woefully bad at statistical analysis. It can hardly be a coincidence that both ‘progressive’ climate scientists and political scientists struggle with statistical concepts.
It’s rather easy to torture statistics to ‘prove’ to the layman (or even the relatively well informed) almost anything, once you have decided what your end result ‘should’ be. Most of us are familiar with the embarrassment of Mann’s “Hockey Stick”.
Comments are closed.